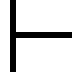Теорема Карри (свойство экстенсиональности)

Теории λ+ext и λη эквивалентны.

Доказательство

λ+ext 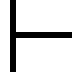λη (η-конверсия не нарушает равенства)

Пусть (λx. v x) →_η v, где x ∉ FV(v).
Рассмотрим терм (λx. v x) y, где y - новая переменная, y ∉ FV(v)

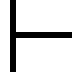λη λ+ext

Пусть u x = v x, где x ∉ FV(u) ∪ FV(v).

⇒ λx. u x = λx. v x	; правило ξ
⇒ u = v	; правило η дважды