если w ≡ x, то COMB(λx. x) ≡ I;
если w ≡ y (x
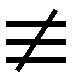 y),
то COMB(λx. y) ≡ К y.
y),
то COMB(λx. y) ≡ К y.
Тогда по предположению индукции существуют термы u' и v' без абстрактора, такие что u' ≡ COMB(λx.u) и v' ≡ COMB(λx.v).
Положим COMB(λx.u v) ≡ Su' v'.
Теорема. Для каждого лямбда-терма существует эквивалент без λ-абстракций с теми же свободными переменными, записанный с помощью комбинаторов (комбинáторное выражение).
Определим конструктивно процедуру COMB, которая по произвольному терму строит соответствующее комбинаторное выражение.
Если терм u не содержит абстрактора λ, очевидно
COMB(u) ≡ u.
Для произвольного терма вида λx. w процедура определим индуктивно по построению терма.
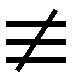 y),
то COMB(λx. y) ≡ К y.
y),
то COMB(λx. y) ≡ К y.