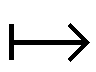 x², g: x
x², g: x 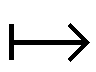 2x
2xD f = g,
Говоря f(x)
, что подразумевают:
В математической статье из контекста понятно, для формального исследования необходима точность. Лямбда-нотация предложена Алонзо Чёрчем в 1930 г.
(x²)' = 2x
Подставив в обе части x := 1, получим
| (1²)' = 2' = 0 | 2 ⋅ 1 = 2 |
В действительности мы имеем равенство двух функций, а не чисел
f: x 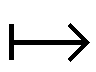 x², g: x
x², g: x 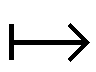 2x
2x
D f = g,
где D - оператор дифференцирования (абстрагируемся от необходимости того, что f должна быть дифференцируемой). Он имеет тип
D ∈ [[R→R]→[R→R]]
Можно записать в виде безымянных функций:
D (x 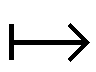 x²) = (x
x²) = (x 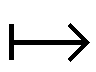 2x)
2x)
λ-нотация — замена стрелки 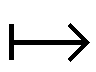 : f = λx.x²
: f = λx.x²